![]()
Этот способ весьма распространен и состоит в том, чтобы преобразовать исходное уравнение к виду F(f(х)) =0, где F(t) – некоторый многочлен, а f(х) – одна из тригонометрических функций. Требуется с помощью тригонометрических тождеств выразить все тригонометрические функции, участвующие в рассматриваемом уравнении, через одну какую-нибудь простейшую тригонометрическую функцию. Приведем примеры.
![]()
Пример1. Решить уравнение 2соs2 х + 5sin х -4 =0
Решение. Если cos2х=1-sin2х, то уравнение приводится к квадратному уравнению относительно sin х:
2(1- sin2х) + 5sinх-4 = 0,
раскрываем скобки, переносим все в левую часть, получим
2 sin2х - 5sinх+2 = 0,
заменим sin х = y, уравнение примет вид
2y2 - 5y + 2 = 0.
Это уравнение является квадратным. Находим корни уравнения:
![]() ;
;
![]() .
.
Так как у=sinх, то
![]()
или
![]()
Тогда:
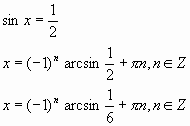 ,
,
sinх=2 не имеет решения, так как ½ sinх½ £ 1.
Ответ:
![]()
Пример2. Решить уравнение соs4 х - sin 4х= sin х
Решение. Представим левую часть уравнения как разность квадратов, получим:
(соs2 х + sin2 х)( соs2 х - sin2 х) = sin х;
учитывая, что
соs2 х + sin2 х=1, а соs2 х - sin2 х = 1-2 sin2х,
подставим в исходное уравнение.
Теперь уравнение принимает вид:
1 - 2 sin2 х – sin х = 0 или 2 sin2 х + sin х -1 = 0.
Если заменить sin х = у, получим квадратное уравнение вида:
2у2 + у – 1 = 0.
Находим корни квадратного уравнения
![]()
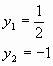
Получим:
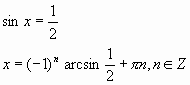
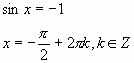
Объединив эти решения, получим
Полученные корни уравнения нанесены на рисунок 2, что позволяет наглядно увидеть результат решения, которое можно выразить следующим образом
![]()
Такая запись является более короткой формой преставления корней решения уравнения.
Ответ:
![]()
Пример3. Решить уравнение 6tg х + 5сtg3х = tg 2х
Решение. ОДЗ: соsх¹ 0; sin3х¹ 0; соs2х¹ 0.
Запишем уравнение в виде 5tg х + 5сtg3х = tg 2х- tg х и подставим в него
![]() ,
,
![]() ,
,
получим:
![]() .
.
Приводим к общему знаменателю обе части уравнения :
![]()
Числитель левой части уравнения можно представить как косинус суммы двух углов, а числитель правой части – как синус разности двух углов:
![]() ,
,
или
![]() ,
,
5соs22х= sinх ×sin3х.
Представим правую часть уравнения в виде полу разности косинусов, получим:
5соs22х=1/2 (соs2х–cos4х) ,
умножим обе части равенства на 2 и перенесем все в левую часть :
10соs22х - соs2х + cos 4х = 0,
соs4х представим как косинус двойного угла:
10соs22х-соs2х+(2cos22х-1)=0, отсюда 12соs22х-соs2х-1=0,
заменим соs2х=у, получим квадратное уравнение вида 12у2 – у – 1 = 0, находим корни :
![]() ,
,
![]() ,
,
подставив вместо у=соs2х, получим:
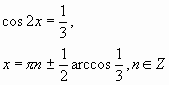
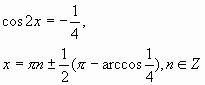
Оба корня входят в ОДЗ.
Ответ :
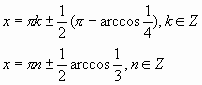
![]()