phobos.jpg (14475 bytes)Гравитационное поле Фобоса

 

Кавендишева гравитационная постоянная G = (6.6745 ± 0.0008) . 10 -8 см / г.с2.

Общие сведения

Физическая величина

Числовое значение

 Размерность Ссылка
 Объем Фобоса */  5628 ± 50 км3 [1]
 Средний радиус **/ 11.03±0.04 км  
 Полуоси трехосного эллипсоида ***/  a = (13.5 ± 1), b = (10.7 ± 1), с = (9.6 ± 1) км [2]
 Фобосоцентрическая гравитационная постоянная GMф  0.00066 ± 0.00004  км3/c2 [3]
 Масса Фобоса М  (9.9 ± 0.6) . 10 18  г  
 Средняя плотность  1.76 ± 0.11 м  
 Угловая скорость суточного вращения Фобоса    ω = 2π / T  0.00022792  рад/с  
 Период суточного вращения  7 h 39m 27s    
 Среднее ускорение силы тяжести   мгал  

*/ Объем Фобоса вычислен по заданным координатам точек поверхности
**/ Средний радиус Фобоса определен как радиус сферы, объем которой равен объему Фобоса
***/ Общая геометрическая фигура Фобоса близка к трехосному эллипсоиду, полуоси которого приведены в таблице.

Период суточного вращения  совпадает с периодом обращения Фобоса вокруг Марса. Поэтому Фобос всегда обращен к Марсу одной стороной, в направлении которой находится наибольшая полуось.

Потенциал притяжения Фобоса в виде ряда по сферическим функциям

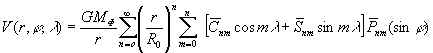
grav_p4.jpg (4595 bytes)

где GMф - фобосоцентрическая гравитационная постоянная,
r, φ, λ - координаты точек пространства, где рассматривается потенциал,
Pnm (sin φ) - нормированные присоединенные функции Лежандра.

Нормированные гармонические коэффициенты вычислялись по формуле

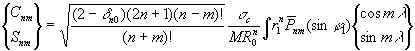
g_p1.jpg (5553 bytes)

где  δno - символ Кронекера,   σc - значение средней плотности.

Нормированные гармонические коэффициенты  Ĉnm и  Ŝnm  гравитационного потенциала Фобоса и ошибки их определения

n

m

 Ĉnm

±σĈnm

  Ŝnm

±σŜnm

0 0    0,9999 0,0026   0 0
1 0   -0,0324 0,0020   0 0
1 1   -0,0390 0,0026   0,0089 0,0021
2 0   -0,2164 0,0022   0 0
2 1    0,0146 0,0020 -0,0058 0,0030
2 2    0,2134 0,0028 -0,0317 0,0018
3 0    0,0091 0,0020   0 0
3 1    0,0163 0,0022   0,0140 0,0020
3 2   -0,0273 0,0023   0,0146 0,0018
3 3   -0,0218 0,0021 -0,0179 0,0029
4 0     0,0476 0,0027   0 0
4 1    -0,0009 0,0030   0,0054 0,0019
4 2    -0,0479 0,0036 -0,0271 0,0025
4 3    -0,0193 0,0025 -0,0054   0,0025
4 4     0,0508 0,0040 -0,0298    0,0033
5 0     0,0345 0,0026   0    0
5 1    -0,0166 0,0020 -0,0124 0,0013
5 2    -0,0195 0,0015   0,0247   0,0016
5 3     0,0045 0,0028   0,0279    0,0034
5 4   -0,0074 0,0026   0,0071   0,0024
5 5   -0,0307 0,0042 -0,0203 0,0050
6 0   -0,0259 0,0034   0 0
6 1   -0,0116 0,0042 -0,0012 0,0017
6 2    0,0259 0,0040   0,0267    0,0037
6 3    0,0166 0,0035 -0,0047   0,0030
6 4    -0,0197 0,0031 -0,0067 0,0040
6 5    -0,0335 0,0046   0,0018   0,0036
6 6     0,0035 0,0048 -0,0036   0,0048

 
Сайт создан в системе uCoz