![]()
Определение. Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным.
Решаются такие уравнения делением левой и правой части на sinх или соsх соответствующей степени. Если считать sinх и соsх - члены первой степени, то каждое слагаемое должно иметь одинаковую степень, такие уравнения называются однородными. Предварительно проверив, что если соs х = 0 (или sinх =0) является решением, то его надо включить в ответ.
Рассмотрим такой метод решения тригонометрических уравнений на примерах:
![]()
Пример1. Решить уравнение соs3х+ sin3х =0, где соs 3х=0 не является решением уравнения.
Решение. Делим обе части уравнения на соs3х:
![]() ,
,
1 + tg3х=0,
откуда
tg3х=-1,
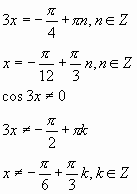
Ответ:
![]()
Пример2. Решить уравнение 6sin2х - sinх× cosх - соs2х=3
Решение. Это уравнение второй степени. Представим 1= sin2х +cos2х, тогда уравнение примет вид:
6sin 2х- sinх cosх- соs 2х=3(sin2х +cos2х).
После раскрытия скобок получаем:
6sin 2х - sinх cosх - соs 2х - 3sin2х -3cos2х=0,
Преобразуем полученное уравнение:
3sin 2х- sinх cosх- 4соs 2х=0,
делим обе части уравнения на соs2х.
Так как соsх=0 при
![]()
и не является корнем данного уравнения 3tg2х- tgх-4=0, заменим tgх=у, получим квадратное уравнение вида 3у2-у-4=0, находим корни
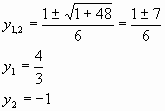
Тогда:
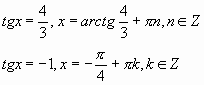
Ответ:
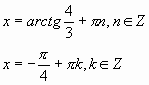
![]()